Block program as a standalone solver¶
In the following DMRG calculation, C2 molecule is used to demonstrate various computational features as of the 1.5.2 release. Integrals and orbitals must be supplied externally in Molpro’s FCIDUMP format. The integral files for C2 can be found here: FCIDUMP or generated by the PySCF script:
from pyscf import gto, scf, mcscf, dmrgscf
mol = gto.M(atom='C 0 0 0; C 0 0 1.2425', basis='ccpvdz', symmetry=1)
mf = scf.RHF(mol).run()
mc = mcscf.CASCI(mf, 26, 8)
mc.fcisolver = dmrgscf.DMRGCI(mol)
dmrgscf.dryrun(mc)
Molecular symmetry¶
Example 1: BLOCK input with the default settings for the ground state energy:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
hf_occ integral
schedule default
maxM 500
maxiter 30
D2h symmetry is enabled by sym d2h.
The simplest option is to take schedule default and the maximum number of renormalized states, maxM.
BLOCK will then automatically choose a sweep schedule as well as set defaults for various tolerances.
The discarded weights and associated sweep energies can be extracted by grepping output.dat, for instance:
$ grep "Sweep Energy" output.dat
M = 250 state = 0 Largest Discarded Weight = 2.601e-05 Sweep Energy = -75.7044175965
M = 250 state = 0 Largest Discarded Weight = 4.145e-05 Sweep Energy = -75.7253836704
M = 250 state = 0 Largest Discarded Weight = 5.085e-05 Sweep Energy = -75.7268081556
M = 250 state = 0 Largest Discarded Weight = 5.615e-05 Sweep Energy = -75.7271779408
M = 250 state = 0 Largest Discarded Weight = 5.769e-05 Sweep Energy = -75.7272098184
M = 250 state = 0 Largest Discarded Weight = 5.568e-05 Sweep Energy = -75.7273283072
M = 250 state = 0 Largest Discarded Weight = 5.712e-05 Sweep Energy = -75.7273267274
M = 250 state = 0 Largest Discarded Weight = 5.517e-05 Sweep Energy = -75.7273439451
M = 500 state = 0 Largest Discarded Weight = 1.441e-05 Sweep Energy = -75.7278969832
M = 500 state = 0 Largest Discarded Weight = 1.504e-05 Sweep Energy = -75.7281427759
M = 500 state = 0 Largest Discarded Weight = 3.768e-06 Sweep Energy = -75.7282950558
M = 500 state = 0 Largest Discarded Weight = 4.737e-06 Sweep Energy = -75.7283534344
M = 500 state = 0 Largest Discarded Weight = 4.602e-13 Sweep Energy = -75.7283427167
M = 500 state = 0 Largest Discarded Weight = 8.882e-16 Sweep Energy = -75.7283455434
M = 500 state = 0 Largest Discarded Weight = 3.689e-13 Sweep Energy = -75.7283467279
State wavefunction¶
BLOCK can target the states distinguished by the number of electrons nelec, the total spin spin and the point-group symmetry of the state irrep.
Example 2: a single B1g state in D2h:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 4
hf_occ integral
schedule default
maxM 500
maxiter 30
Extract energies running:
$ grep "Sweep Energy" output.dat
M = 250 state = 0 Largest Discarded Weight = 2.074e-05 Sweep Energy = -75.5487622154
M = 250 state = 0 Largest Discarded Weight = 2.572e-05 Sweep Energy = -75.6216559252
M = 250 state = 0 Largest Discarded Weight = 3.001e-05 Sweep Energy = -75.6377863834
M = 250 state = 0 Largest Discarded Weight = 3.869e-05 Sweep Energy = -75.6380712454
M = 250 state = 0 Largest Discarded Weight = 3.410e-05 Sweep Energy = -75.6381445876
M = 250 state = 0 Largest Discarded Weight = 3.936e-05 Sweep Energy = -75.6381956325
M = 250 state = 0 Largest Discarded Weight = 3.597e-05 Sweep Energy = -75.6381986704
M = 250 state = 0 Largest Discarded Weight = 3.956e-05 Sweep Energy = -75.6382158943
M = 500 state = 0 Largest Discarded Weight = 4.035e-06 Sweep Energy = -75.6386091307
M = 500 state = 0 Largest Discarded Weight = 9.904e-06 Sweep Energy = -75.6387867388
M = 500 state = 0 Largest Discarded Weight = 1.011e-06 Sweep Energy = -75.6388951005
M = 500 state = 0 Largest Discarded Weight = 1.909e-06 Sweep Energy = -75.6389530440
M = 500 state = 0 Largest Discarded Weight = 8.626e-14 Sweep Energy = -75.6389616714
M = 500 state = 0 Largest Discarded Weight = 7.772e-16 Sweep Energy = -75.6389641931
M = 500 state = 0 Largest Discarded Weight = 8.882e-16 Sweep Energy = -75.6389650943
M = 500 state = 0 Largest Discarded Weight = 1.332e-15 Sweep Energy = -75.6389656999
M = 500 state = 0 Largest Discarded Weight = 8.882e-16 Sweep Energy = -75.6389659838
State-averaged calculation¶
A state-averaged DMRG is available in BLOCK for which more than a single state can be targeted in the same calculation.
Currently the states being calculated must be of the same irrep.
The number of roots and the weight of each state can be specified by nroots and weights, respectively.
Example 3: a state-averaged DMRG of two Ag states in D2h:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
nroots 2
weights 0.5 0.5
hf_occ integral
schedule default
maxM 500
maxiter 30
Extract energies running:
$ grep "Sweep Energy" output.dat
M = 250 state = 0 Largest Discarded Weight = 3.301e-05 Sweep Energy = -75.6977658954
M = 250 state = 1 Largest Discarded Weight = 3.301e-05 Sweep Energy = -75.6097171207
M = 250 state = 0 Largest Discarded Weight = 1.210e-04 Sweep Energy = -75.7242895778
M = 250 state = 1 Largest Discarded Weight = 1.210e-04 Sweep Energy = -75.6351366904
M = 250 state = 0 Largest Discarded Weight = 7.977e-05 Sweep Energy = -75.7258318951
M = 250 state = 1 Largest Discarded Weight = 7.977e-05 Sweep Energy = -75.6364792592
M = 250 state = 0 Largest Discarded Weight = 1.510e-04 Sweep Energy = -75.7262492462
M = 250 state = 1 Largest Discarded Weight = 1.510e-04 Sweep Energy = -75.6369788516
M = 250 state = 0 Largest Discarded Weight = 8.775e-05 Sweep Energy = -75.7262820781
M = 250 state = 1 Largest Discarded Weight = 8.775e-05 Sweep Energy = -75.6369957594
M = 250 state = 0 Largest Discarded Weight = 1.508e-04 Sweep Energy = -75.7263169403
M = 250 state = 1 Largest Discarded Weight = 1.508e-04 Sweep Energy = -75.6370412456
M = 250 state = 0 Largest Discarded Weight = 8.819e-05 Sweep Energy = -75.7263181429
M = 250 state = 1 Largest Discarded Weight = 8.819e-05 Sweep Energy = -75.6370413712
M = 250 state = 0 Largest Discarded Weight = 1.507e-04 Sweep Energy = -75.7263184125
M = 250 state = 1 Largest Discarded Weight = 1.507e-04 Sweep Energy = -75.6370456106
M = 500 state = 0 Largest Discarded Weight = 2.841e-05 Sweep Energy = -75.7274562077
M = 500 state = 1 Largest Discarded Weight = 2.841e-05 Sweep Energy = -75.6382052116
M = 500 state = 0 Largest Discarded Weight = 4.424e-05 Sweep Energy = -75.7277476086
M = 500 state = 1 Largest Discarded Weight = 4.424e-05 Sweep Energy = -75.6385132723
M = 500 state = 0 Largest Discarded Weight = 1.542e-05 Sweep Energy = -75.7279342967
M = 500 state = 1 Largest Discarded Weight = 1.542e-05 Sweep Energy = -75.6386584359
M = 500 state = 0 Largest Discarded Weight = 2.401e-05 Sweep Energy = -75.7279737606
M = 500 state = 1 Largest Discarded Weight = 2.401e-05 Sweep Energy = -75.6386894476
M = 500 state = 0 Largest Discarded Weight = 1.109e-05 Sweep Energy = -75.7279250579
M = 500 state = 1 Largest Discarded Weight = 1.109e-05 Sweep Energy = -75.6386605282
M = 500 state = 0 Largest Discarded Weight = 1.408e-05 Sweep Energy = -75.7279222935
M = 500 state = 1 Largest Discarded Weight = 1.408e-05 Sweep Energy = -75.6386563064
M = 500 state = 0 Largest Discarded Weight = 8.824e-06 Sweep Energy = -75.7279257860
M = 500 state = 1 Largest Discarded Weight = 8.824e-06 Sweep Energy = -75.6386550817
M = 500 state = 0 Largest Discarded Weight = 1.389e-05 Sweep Energy = -75.7279257093
M = 500 state = 1 Largest Discarded Weight = 1.389e-05 Sweep Energy = -75.6386552913
M = 500 state = 0 Largest Discarded Weight = 8.724e-06 Sweep Energy = -75.7279265042
M = 500 state = 1 Largest Discarded Weight = 8.724e-06 Sweep Energy = -75.6386566145
State-specific calculation¶
The state-specific calculation is implemented as a restart calculation which assumes
that a previous DMRG (e.g., state-average) calculation has been converged.
The state-specific DMRG calculation of BLOCK then takes these wave functions and refines them for each root separately.
Currently only “onedot” algorithm is implemented for a state-specific DMRG calculation.
Example 4: a state-specific DMRG of two Ag states consists of two steps.
First, obtain state-averaged wavefunctions as carried out in Example 3.
Second, perform the state-specific DMRG calculation by specifying
statespecificalong with algorithm, reading the previous DMRG wavefunction:sym d2h orbitals FCIDUMP nelec 8 spin 0 irrep 1 nroots 2 weights 0.5 0.5 onedot statespecific hf_occ integral schedule default maxM 500 maxiter 30
Extract energies running:
$ grep "Sweep Energy" output.dat
M = 250 state = 0 Largest Discarded Weight = 1.074e-04 Sweep Energy = -75.7278258618
M = 250 state = 0 Largest Discarded Weight = 6.265e-05 Sweep Energy = -75.7271218843
M = 250 state = 0 Largest Discarded Weight = 7.364e-05 Sweep Energy = -75.7269947744
M = 250 state = 0 Largest Discarded Weight = 5.524e-05 Sweep Energy = -75.7269943736
M = 250 state = 0 Largest Discarded Weight = 7.321e-05 Sweep Energy = -75.7269691045
M = 250 state = 0 Largest Discarded Weight = 5.323e-05 Sweep Energy = -75.7269678846
M = 250 state = 0 Largest Discarded Weight = 7.223e-05 Sweep Energy = -75.7269635922
M = 500 state = 0 Largest Discarded Weight = 2.184e-05 Sweep Energy = -75.7272771612
M = 500 state = 0 Largest Discarded Weight = 3.572e-05 Sweep Energy = -75.7276387065
M = 500 state = 0 Largest Discarded Weight = 9.265e-13 Sweep Energy = -75.7279934002
M = 500 state = 0 Largest Discarded Weight = 4.463e-13 Sweep Energy = -75.7280861611
M = 500 state = 0 Largest Discarded Weight = 5.551e-16 Sweep Energy = -75.7281187446
M = 500 state = 0 Largest Discarded Weight = 9.370e-14 Sweep Energy = -75.7281327072
M = 500 state = 0 Largest Discarded Weight = 3.331e-16 Sweep Energy = -75.7281397782
M = 500 state = 0 Largest Discarded Weight = 9.248e-14 Sweep Energy = -75.7281445745
M = 500 state = 0 Largest Discarded Weight = 6.661e-16 Sweep Energy = -75.7281474895
M = 500 state = 0 Largest Discarded Weight = 9.992e-16 Sweep Energy = -75.7281493387
M = 250 state = 1 Largest Discarded Weight = 8.564e-05 Sweep Energy = -75.6385347218
M = 250 state = 1 Largest Discarded Weight = 5.385e-05 Sweep Energy = -75.6380963835
M = 250 state = 1 Largest Discarded Weight = 6.158e-05 Sweep Energy = -75.6380128961
M = 250 state = 1 Largest Discarded Weight = 4.984e-05 Sweep Energy = -75.6380120359
M = 250 state = 1 Largest Discarded Weight = 5.948e-05 Sweep Energy = -75.6379881607
M = 250 state = 1 Largest Discarded Weight = 4.954e-05 Sweep Energy = -75.6379876616
M = 250 state = 1 Largest Discarded Weight = 6.004e-05 Sweep Energy = -75.6379771996
M = 500 state = 1 Largest Discarded Weight = 2.159e-05 Sweep Energy = -75.6382108002
M = 500 state = 1 Largest Discarded Weight = 2.180e-05 Sweep Energy = -75.6385015895
M = 500 state = 1 Largest Discarded Weight = 4.491e-13 Sweep Energy = -75.6387780117
M = 500 state = 1 Largest Discarded Weight = 6.379e-13 Sweep Energy = -75.6388358995
M = 500 state = 1 Largest Discarded Weight = 1.465e-13 Sweep Energy = -75.6388549910
M = 500 state = 1 Largest Discarded Weight = 7.405e-14 Sweep Energy = -75.6388647713
M = 500 state = 1 Largest Discarded Weight = 1.107e-13 Sweep Energy = -75.6388699886
M = 500 state = 1 Largest Discarded Weight = 1.809e-13 Sweep Energy = -75.6388729422
M = 500 state = 1 Largest Discarded Weight = 2.220e-16 Sweep Energy = -75.6388750897
M = 500 state = 1 Largest Discarded Weight = 6.661e-16 Sweep Energy = -75.6388767670
n-particle reduced density matrix¶
The DMRG reduced density matrix up to the 4-particle type for a particular state can be obtained
by employing the keywords onepdm, twopdm, threepdm and fourpdm.
Currently only “onedot” algorithm is implemented for this type of calculation.
Density matrices of the n-th state are calculated and stored in a text file named spatial_onepdm.n.n.txt, spatial_twopdm.n.n.txt,
spatial_threepdm.n.n.txt and spatial_fourpdm.n.n.txt, respectively, starting with n=0.
Example 5: 2-particle density matrix for the ground state:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
hf_occ integral
schedule default
maxM 500
maxiter 30
twopdm
The 2-particle density matrix is stored in the file of spatial_twopdm.0.0.txt.
Example 6: state-averaged 2-particle density matrix for two roots:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
nroots 2
weights 0.5 0.5
hf_occ integral
schedule default
maxM 500
maxiter 30
twopdm
The 2-particle density matrices for both state 1 and state 2 are stored in the files of spatial_twopdm.0.0.txt, and spatial_twopdm.1.1.txt, respectively.
1- and 2-particle transition reduced density matrix¶
1-particle and 2-particle transition density matrices can be calculated using the keyword tran_onepdm and tran_twopdm.
Transition density matrices between the m-th and n-th states are calculated and stored in a text file named spatial_onepdm.m.n.txt
and spatial_twopdm.m.n.txt, respectively, starting with m=1 and n=0.
The transition density matrices between states with different symmetry irreducible presentations are also available. However, this type of calculation requires multiple steps and the manipulation of scratch files and will be discussed in Restart DMRG transition reduced density matrix calculation.
Example 7: state-averaged 2-particle transition density matrix between two Ag states:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
nroots 2
weights 0.5 0.5
hf_occ integral
schedule default
maxM 500
maxiter 30
tran_twopdm
The state-average 2-particle transition density matrix is stored in the file of spatial_twopdm.1.0.txt.
Example 8: state-specific 2-particle transition density matrix between two refined Ag states:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
nroots 2
weights 0.5 0.5
onedot
statespecific
hf_occ integral
schedule default
maxM 500
maxiter 30
tran_twopdm
The state-specific 2-particle transition density matrix is stored in the file of spatial_twopdm.1.0.txt.
Restart DMRG energy calculation¶
DMRG energy calculations can be restarted, using the .tmp scratch files generated in the previous calculation, by specifying the keyword restart.
Example 9: restart DMRG enegy calculation:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
hf_occ integral
schedule default
maxM 500
maxiter 30
restart
Extract energies running:
$ grep "Sweep Energy" output.dat
M = 500 state = 0 Largest Discarded Weight = 9.792e-14 Sweep Energy = -75.7283469966
M = 500 state = 0 Largest Discarded Weight = 1.221e-15 Sweep Energy = -75.7283469966
M = 500 state = 0 Largest Discarded Weight = 4.441e-16 Sweep Energy = -75.7283469966
M = 500 state = 0 Largest Discarded Weight = 1.332e-15 Sweep Energy = -75.7283469966
M = 500 state = 0 Largest Discarded Weight = 4.441e-16 Sweep Energy = -75.7283469966
Restart DMRG n-particle reduced density matrix calculation¶
Up to 4-particle reduced density matrices can be calculated separately, by restarting from an existing DMRG wave function.
This requires the presence of the following scratch files with .tmp extension: “statefile”, “StateInfo”, “wave” and “Rotation”.
Example 10: restart DMRG 2-particle density matrix calculation:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
hf_occ integral
schedule default
maxM 500
maxiter 30
restart_twopdm
The 2-particle density matrix is stored in the file of spatial_twopdm.0.0.txt.
Restart DMRG transition reduced density matrix calculation¶
A transition density matrix calculation can be carried out separately, by restarting from existing DMRG wave functions of bra and ket states.
Example 11: state-averaged 2-particle transition density matrix between bra and ket states belonging to the same irrep:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
nroots 2
weights 0.5 0.5
hf_occ integral
schedule default
maxM 500
maxiter 30
restart_tran_twopdm
The 2-particle transition density matrix is stored in the file of spatial_twopdm.1.0.txt.
When bra and ket states belong to different irreps, the restart calculation takes a few steps in which the corresponding state-specific calculations are needed.
Example 12: 2-particle transition density matrix between Ag (bra) and B3u (ket) states.
- Carry out state-specific calculations for bra and ket states separately, in different scratch directories of
scratch_braandscratch_ket, enabled by the keywordscratch.BLOCKlabels bra and ket states as “state 1” and “state 0”, respectively.
First, creat the scratch directory by mkdir ./scratch_bra and calculate bra state as “state 1” belonging to irrep 2 of D2h:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 2
hf_occ integral
schedule default
maxM 500
maxiter 30
scratch scratch_bra
Second, creat the scratch directory by mkdir ./scratch_ket and calculate ket state as “state 0” belonging to irrep 1 of D2h:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
hf_occ integral
schedule default
maxM 500
maxiter 30
scratch scratch_ket
In ./scratch_bra, rename the resulting “statefile”, “wave”, “Rotation” scratch files by changing the numbers before the .tmp extension from “0” to “1”:
$ rename .0.tmp .1.tmp *.tmp
$ rename .state0.tmp .state1.tmp Rotation*.tmp
Copy all “statefile”, “wave”, “Rotation”
.tmpfiles fromscratch_braandscratch_ketdirectories to a separate directoryscratch_tranfor restarting calculation.Restart a 2-particle transition density matrix calculation by adding the keyword
restart_tran_twopdm. In additionirrep 2 1represents Ag and B3u states for bra and ket, respectively:sym d2h orbitals FCIDUMP nelec 8 spin 0 irrep 2 1 nroots 2 hf_occ integral schedule default maxM 500 maxiter 30 scratch scratch_tran restart_tran_twopdm
The 2-particle transition density matrix is stored in the file of spatial_twopdm.1.0.txt.
Customize sweep schedule¶
The sweep schedule defines the renormalised states M used in successive DMRG sweeps. For finer control over the sweeps, we recommend using a more advanced input.
Example 13: customized sweep schedule for the ground state of C2 molecule:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
hf_occ integral
schedule
0 100 1e-6 1e-6
4 250 1e-6 1e-6
8 400 1e-6 1e-6
10 600 1e-8 1e-8
12 800 1e-10 1e-10
14 800 1e-10 0.0
end
twodot_to_onedot 16
maxiter 100
sweep_tol 1e-9
Extract energies running:
$ grep "Sweep Energy" output.dat
M = 100 state = 0 Largest Discarded Weight = 3.960e-05 Sweep Energy = -75.6814569486
M = 100 state = 0 Largest Discarded Weight = 8.248e-05 Sweep Energy = -75.7162162063
M = 100 state = 0 Largest Discarded Weight = 1.299e-04 Sweep Energy = -75.7197142506
M = 100 state = 0 Largest Discarded Weight = 1.405e-04 Sweep Energy = -75.7207575174
M = 250 state = 0 Largest Discarded Weight = 3.124e-06 Sweep Energy = -75.7247598640
M = 250 state = 0 Largest Discarded Weight = 2.578e-05 Sweep Energy = -75.7262894828
M = 250 state = 0 Largest Discarded Weight = 2.747e-05 Sweep Energy = -75.7266725035
M = 250 state = 0 Largest Discarded Weight = 3.358e-05 Sweep Energy = -75.7269909475
M = 400 state = 0 Largest Discarded Weight = 2.523e-06 Sweep Energy = -75.7273900910
M = 400 state = 0 Largest Discarded Weight = 8.012e-06 Sweep Energy = -75.7276294430
M = 600 state = 0 Largest Discarded Weight = 7.906e-07 Sweep Energy = -75.7279563319
M = 600 state = 0 Largest Discarded Weight = 2.633e-06 Sweep Energy = -75.7282799011
M = 800 state = 0 Largest Discarded Weight = 5.453e-07 Sweep Energy = -75.7284217562
M = 800 state = 0 Largest Discarded Weight = 1.075e-06 Sweep Energy = -75.7284897369
M = 800 state = 0 Largest Discarded Weight = 1.097e-06 Sweep Energy = -75.7284954448
M = 800 state = 0 Largest Discarded Weight = 1.141e-06 Sweep Energy = -75.7285020635
M = 800 state = 0 Largest Discarded Weight = 1.774e-12 Sweep Energy = -75.7284957831
M = 800 state = 0 Largest Discarded Weight = 1.998e-15 Sweep Energy = -75.7284962879
M = 800 state = 0 Largest Discarded Weight = 1.665e-15 Sweep Energy = -75.7284964775
M = 800 state = 0 Largest Discarded Weight = 8.882e-16 Sweep Energy = -75.7284965570
M = 800 state = 0 Largest Discarded Weight = 9.925e-14 Sweep Energy = -75.7284966051
M = 800 state = 0 Largest Discarded Weight = 9.992e-16 Sweep Energy = -75.7284966429
M = 800 state = 0 Largest Discarded Weight = 4.441e-16 Sweep Energy = -75.7284966756
M = 800 state = 0 Largest Discarded Weight = 9.992e-16 Sweep Energy = -75.7284967027
M = 800 state = 0 Largest Discarded Weight = 9.837e-14 Sweep Energy = -75.7284967230
M = 800 state = 0 Largest Discarded Weight = 5.551e-16 Sweep Energy = -75.7284967374
M = 800 state = 0 Largest Discarded Weight = 9.714e-14 Sweep Energy = -75.7284967475
M = 800 state = 0 Largest Discarded Weight = 6.661e-16 Sweep Energy = -75.7284967548
M = 800 state = 0 Largest Discarded Weight = 9.781e-14 Sweep Energy = -75.7284967604
M = 800 state = 0 Largest Discarded Weight = 8.882e-16 Sweep Energy = -75.7284967649
M = 800 state = 0 Largest Discarded Weight = 1.665e-15 Sweep Energy = -75.7284967687
M = 800 state = 0 Largest Discarded Weight = 1.221e-15 Sweep Energy = -75.7284967719
M = 800 state = 0 Largest Discarded Weight = 1.110e-15 Sweep Energy = -75.7284967748
M = 800 state = 0 Largest Discarded Weight = 1.110e-15 Sweep Energy = -75.7284967775
M = 800 state = 0 Largest Discarded Weight = 3.331e-16 Sweep Energy = -75.7284967800
M = 800 state = 0 Largest Discarded Weight = 7.772e-16 Sweep Energy = -75.7284967824
M = 800 state = 0 Largest Discarded Weight = 1.443e-15 Sweep Energy = -75.7284967849
M = 800 state = 0 Largest Discarded Weight = 1.665e-15 Sweep Energy = -75.7284967873
M = 800 state = 0 Largest Discarded Weight = 4.441e-16 Sweep Energy = -75.7284967898
M = 800 state = 0 Largest Discarded Weight = 8.882e-16 Sweep Energy = -75.7284967922
M = 800 state = 0 Largest Discarded Weight = 2.109e-15 Sweep Energy = -75.7284967947
M = 800 state = 0 Largest Discarded Weight = 6.661e-16 Sweep Energy = -75.7284967971
M = 800 state = 0 Largest Discarded Weight = 8.882e-16 Sweep Energy = -75.7284967994
M = 800 state = 0 Largest Discarded Weight = 1.443e-15 Sweep Energy = -75.7284968017
M = 800 state = 0 Largest Discarded Weight = 2.220e-16 Sweep Energy = -75.7284968038
M = 800 state = 0 Largest Discarded Weight = 1.332e-15 Sweep Energy = -75.7284968058
M = 800 state = 0 Largest Discarded Weight = 1.554e-15 Sweep Energy = -75.7284968077
M = 800 state = 0 Largest Discarded Weight = 1.221e-15 Sweep Energy = -75.7284968095
M = 800 state = 0 Largest Discarded Weight = 5.551e-16 Sweep Energy = -75.7284968112
M = 800 state = 0 Largest Discarded Weight = 4.441e-16 Sweep Energy = -75.7284968128
M = 800 state = 0 Largest Discarded Weight = 9.992e-16 Sweep Energy = -75.7284968142
M = 800 state = 0 Largest Discarded Weight = 4.441e-16 Sweep Energy = -75.7284968156
M = 800 state = 0 Largest Discarded Weight = 8.882e-16 Sweep Energy = -75.7284968168
M = 800 state = 0 Largest Discarded Weight = 6.661e-16 Sweep Energy = -75.7284968179
M = 800 state = 0 Largest Discarded Weight = 6.661e-16 Sweep Energy = -75.7284968189
M = 800 state = 0 Largest Discarded Weight = 8.882e-16 Sweep Energy = -75.7284968198
M = 800 state = 0 Largest Discarded Weight = 1.887e-15 Sweep Energy = -75.7284968206
M = 800 state = 0 Largest Discarded Weight = 1.887e-15 Sweep Energy = -75.7284968213
M = 800 state = 0 Largest Discarded Weight = 6.661e-16 Sweep Energy = -75.7284968219
M = 800 state = 0 Largest Discarded Weight = 7.772e-16 Sweep Energy = -75.7284968225
M = 800 state = 0 Largest Discarded Weight = 1.554e-15 Sweep Energy = -75.7284968230
M = 800 state = 0 Largest Discarded Weight = 6.661e-16 Sweep Energy = -75.7284968234
M = 800 state = 0 Largest Discarded Weight = 1.887e-15 Sweep Energy = -75.7284968238
twodot_to_onedot specifies the sweep at which the switch is made
from a twodot to a onedot algorithm.
maxiter gives the maximum number of sweep iterations to be performed.
sweep_tol gives the final tolerance on the DMRG energy,
and is analogous to an energy convergence threshold in other quantum chemistry methods.
In Example 13 between schedule and end each line has four values corresponding to sweep_iteration, M, Davidson_tolerance and Noise, respectively.
sweep_iteration is the sweep iteration in which the number of renormalized states M,
the tolerance of Davidson algorithm and the perturbative noise should take effect.
Sweep energy extrapolation¶
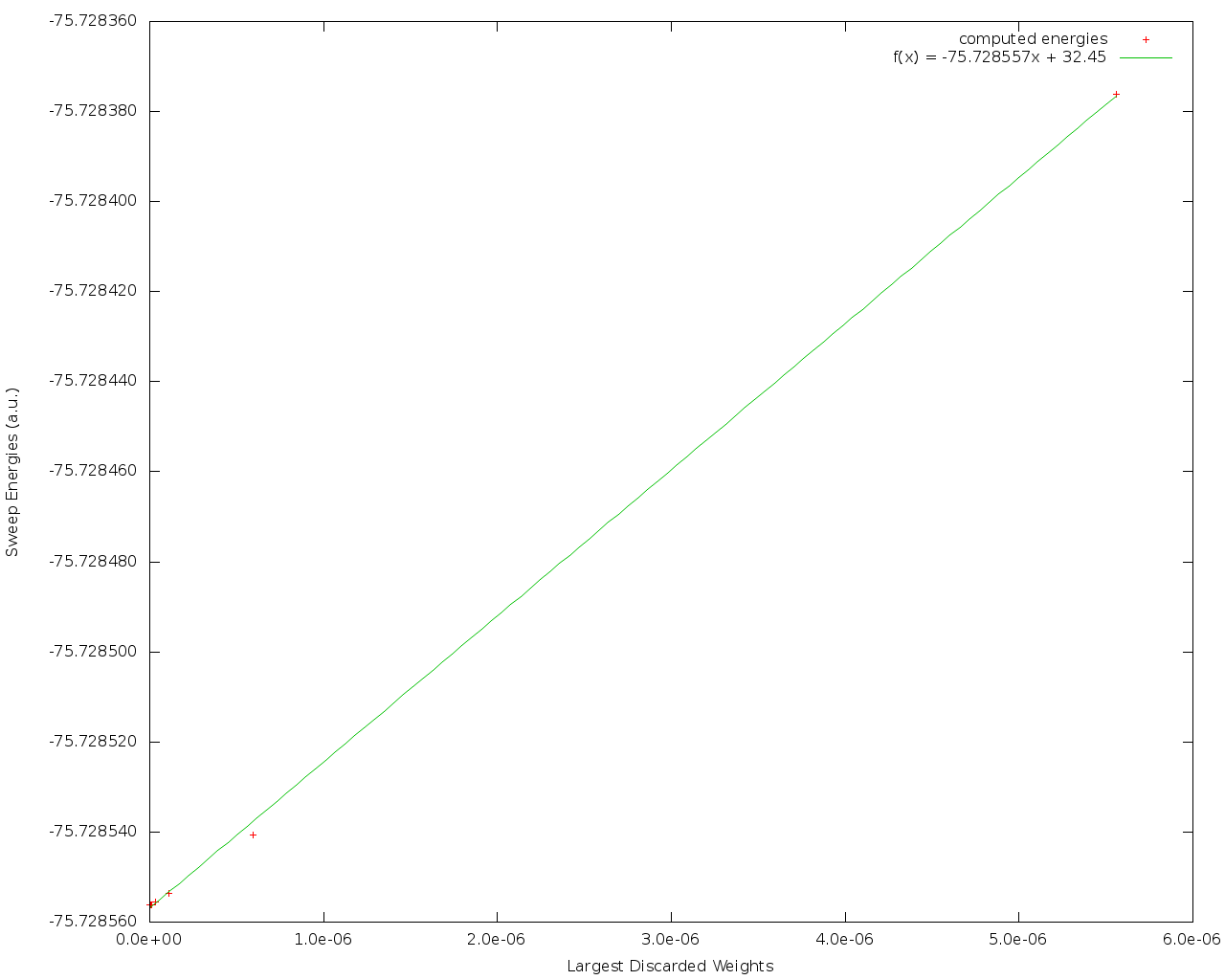
In practice the sweep energy converges almost linearly as a function of the “discarded weight”. Therefore it is convenient to use the “discarded weight” quantity as an estimate of the error of the DMRG calculation. It is recommended to use “twodot” algorithm for energy extrapolation since the “twodot” DMRG wavefunction provides additional variational freedom over the “onedot” DMRG wavefunction. A strong deviation from a linear function (e.g. a plateau behaviour followed by a sudden drop of the energy as a function of discarded weight) indicates that the DMRG was stuck in a local minimum.
Example 14: the ground state of C2, cc-pVDZ basis and customized sweep schedule.
Prepare input.dat:
sym d2h
orbitals FCIDUMP
nelec 8
spin 0
irrep 1
hf_occ integral
schedule
0 250 1.0e-5 1.0e-4
8 500 1.0e-6 1.0e-5
10 500 1.0e-7 1.0e-6
12 1000 1.0e-7 1.0e-7
16 1500 1.0e-7 1.0e-7
20 2000 1.0e-7 1.0e-7
24 2500 1.0e-7 1.0e-7
28 3000 1.0e-7 1.0e-7
32 3500 1.0e-7 1.0e-7
36 4000 1.0e-7 1.0e-7
40 4500 1.0e-7 0.0
end
maxiter 100
sweep_tol 1e-7
Then run BLOCK:
$ block.spin_adapted input.dat > output.dat
When the calculation is done, extract the sweep energies from output.dat:
$ grep "Sweep Energy" output.dat
M = 250 state = 0 Largest Discarded Weight = 2.601e-05 Sweep Energy = -75.7044175965
M = 250 state = 0 Largest Discarded Weight = 4.145e-05 Sweep Energy = -75.7253836704
M = 250 state = 0 Largest Discarded Weight = 5.085e-05 Sweep Energy = -75.7268081556
M = 250 state = 0 Largest Discarded Weight = 5.615e-05 Sweep Energy = -75.7271779408
M = 250 state = 0 Largest Discarded Weight = 5.769e-05 Sweep Energy = -75.7272098184
M = 250 state = 0 Largest Discarded Weight = 5.568e-05 Sweep Energy = -75.7273283072
M = 250 state = 0 Largest Discarded Weight = 5.712e-05 Sweep Energy = -75.7273267274
M = 250 state = 0 Largest Discarded Weight = 5.517e-05 Sweep Energy = -75.7273439451
M = 500 state = 0 Largest Discarded Weight = 2.342e-06 Sweep Energy = -75.7279482411
M = 500 state = 0 Largest Discarded Weight = 6.584e-06 Sweep Energy = -75.7282540320
M = 500 state = 0 Largest Discarded Weight = 4.624e-06 Sweep Energy = -75.7283335685
M = 500 state = 0 Largest Discarded Weight = 5.559e-06 Sweep Energy = -75.7283761594
M = 1000 state = 0 Largest Discarded Weight = 6.188e-08 Sweep Energy = -75.7284812770
M = 1000 state = 0 Largest Discarded Weight = 5.381e-07 Sweep Energy = -75.7285301147
M = 1000 state = 0 Largest Discarded Weight = 5.417e-07 Sweep Energy = -75.7285372992
M = 1000 state = 0 Largest Discarded Weight = 5.967e-07 Sweep Energy = -75.7285405838
M = 1500 state = 0 Largest Discarded Weight = 3.754e-08 Sweep Energy = -75.7285498358
M = 1500 state = 0 Largest Discarded Weight = 1.081e-07 Sweep Energy = -75.7285529289
M = 1500 state = 0 Largest Discarded Weight = 8.351e-08 Sweep Energy = -75.7285532135
M = 1500 state = 0 Largest Discarded Weight = 1.090e-07 Sweep Energy = -75.7285536128
M = 2000 state = 0 Largest Discarded Weight = 1.439e-08 Sweep Energy = -75.7285550762
M = 2000 state = 0 Largest Discarded Weight = 3.133e-08 Sweep Energy = -75.7285555795
M = 2000 state = 0 Largest Discarded Weight = 2.453e-08 Sweep Energy = -75.7285555897
M = 2000 state = 0 Largest Discarded Weight = 3.194e-08 Sweep Energy = -75.7285556424
M = 2500 state = 0 Largest Discarded Weight = 6.035e-09 Sweep Energy = -75.7285560031
M = 2500 state = 0 Largest Discarded Weight = 1.047e-08 Sweep Energy = -75.7285561192
M = 2500 state = 0 Largest Discarded Weight = 8.973e-09 Sweep Energy = -75.7285561321
M = 2500 state = 0 Largest Discarded Weight = 1.026e-08 Sweep Energy = -75.7285561411
M = 3000 state = 0 Largest Discarded Weight = 3.163e-09 Sweep Energy = -75.7285562237
M = 3000 state = 0 Largest Discarded Weight = 4.145e-09 Sweep Energy = -75.7285562440
M = 3000 state = 0 Largest Discarded Weight = 3.361e-09 Sweep Energy = -75.7285562445
M = 3000 state = 0 Largest Discarded Weight = 4.119e-09 Sweep Energy = -75.7285562494
M = 3500 state = 0 Largest Discarded Weight = 1.743e-09 Sweep Energy = -75.7285562638
M = 3500 state = 0 Largest Discarded Weight = 1.691e-09 Sweep Energy = -75.7285562675
M = 3500 state = 0 Largest Discarded Weight = 1.605e-09 Sweep Energy = -75.7285562590
M = 3500 state = 0 Largest Discarded Weight = 1.288e-09 Sweep Energy = -75.7285562542
M = 4000 state = 0 Largest Discarded Weight = 9.977e-10 Sweep Energy = -75.7285562726
M = 4000 state = 0 Largest Discarded Weight = 8.928e-10 Sweep Energy = -75.7285562816
M = 4000 state = 0 Largest Discarded Weight = 7.882e-10 Sweep Energy = -75.7285562783
M = 4000 state = 0 Largest Discarded Weight = 8.000e-10 Sweep Energy = -75.7285562771
M = 4500 state = 0 Largest Discarded Weight = 8.562e-13 Sweep Energy = -75.7285562762
M = 4500 state = 0 Largest Discarded Weight = 1.733e-13 Sweep Energy = -75.7285562762
M = 4500 state = 0 Largest Discarded Weight = 4.441e-16 Sweep Energy = -75.7285562762
M = 4500 state = 0 Largest Discarded Weight = 1.998e-15 Sweep Energy = -75.7285562762
M = 4500 state = 0 Largest Discarded Weight = 7.772e-16 Sweep Energy = -75.7285562762
Energy extrapolation:
Further Reading¶
Some practical questions are often asked such as,
- what sort of molecules can the DMRG be practically applied to?
- what sort of accuracies can be obtained and at what cost? What are the typical sizes of systems (e.g. number of active orbitals) that can be treated with practical computational resources?
- how do we reason about the accuracy of DMRG calculations for dirent molecules?
- how is a DMRG calculation best specified (e.g. in terms of starting orbitals and their order)?
We provide answers in the following paper from both theoretical reasoning and numerical calculation by applying the DMRG
to a representative set of molecules.
The calculations we describe therein are all run in a completely black-box fashion using the default settings of our Block code.
- Olivares-Amaya, W. Hu, N. Nakatani, S. Sharma, J. Yang and G. K.-L. Chan, J. Chem. Phys. 142, 034102 (2015).